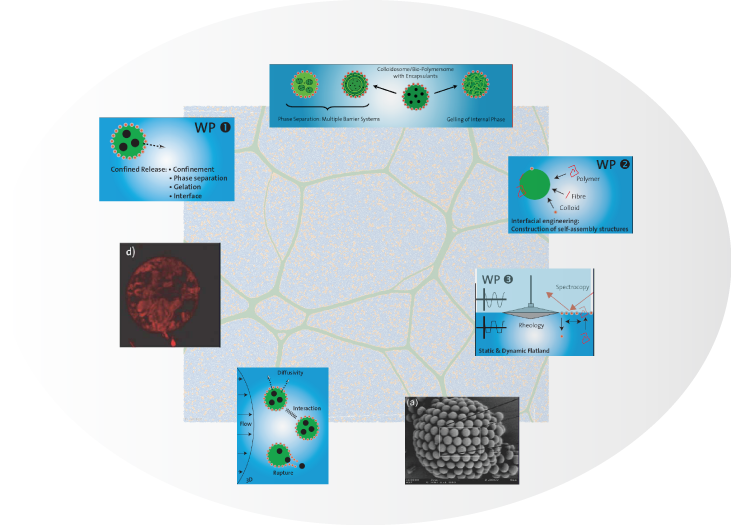
New controlled release systems produced by self-assembly of biopolymers and colloidal particles at fluid-fluid interfaces
| We propose a rational approach to approximating the various alignment tensors. It preserves the correct symmetry and leads to consistent results. For the case of uniaxial nematic fluids, the decoupling approximation for a tensor of rank n involves (n - 2)/2 scalar functions S-n (S-2) in terms of a scalar argument S-2, with S-n(0) = 0 and S-n(1) = 1. Nothing else can be concluded about the mathematical relationship between moments of the distribution function, and in particular, all consistent decoupling approximations for fourth-order moment in terms of second-order moments can be characterized by a single S-4(S2) function. We propose using the simple model dependent convex shaped equilibrium relationship between S-4 and S-2 to characterize new (and simple) decoupling approximations K-I and K-II for the biaxial (including uniaxial) phase. In order to test the new against earlier proposed approximations rigorously, and to discuss consistency issues, we solve the Hess-Doi Fokker-Planck equation for nematic and nematic-discotic liquid crystals efficiently for a wide range of (2300 distinct) possible conditions including mixed shear and elongational flows, diverse field strengths, and molecular shapes. As a result, we confirm the closures K-I and K-II with correct tensorial symmetry; they are valid under arbitrary conditions to high precision, exact in the isotropic and totally aligned phases, improve upon earlier parameter-free closures in particular in the temperature regime T is an element of [0.6, infinity] x T-NI with the nematic-isotropic transition temperature T-NI (or alternatively, for mean-field strengths U is an element of [0, 8]). K-II performs as good as the so-called Bingham closure, which usually requires 30 empirical coefficients, while K-I and K-H are essentially parameter-free, and their quality can be expected to be insensitive to the particular model. (c) 2007 Elsevier B.V. All fights reserved. [hide]
Scientific Board
Scientific Stuff
Associated Scientists |
|
Enjoy your reading
SY Tee, AR Bausch, PA Janmey, | |
Selected conferences (co-)organized by project members8th World Congress on Computational Mechanics WCCM8 200830 June - 5 July 2007, Venice, Italy ► |
13 May 2025
![]() mk
mk